3. Normlar ve Mesafeler

12 Ekim 2025

13 dakika

120 görüntüleme

Normlar ve mesafeler, yapay zekanın veri vektörlerinin "büyüklüğünü" ölçmesini ve aralarındaki farklılıkları ya da benzerlikleri anlamlandırmasını sağlayan temel ölçüm araçlarıdır. Bu makalede, en yaygın kullanılan Öklid (L²), Manhattan (L¹) ve Chebyshev (L-Sonsuz) ailelerini, hem norm hem de mesafe kavramları üzerinden yapay zeka uygulamaları perspektifiyle inceleyeceğiz.

Norm ve Mesafe Nedir?

Vektörleri ve matrisleri anladık; artık elimizde veriyi temsil eden ve onu dönüştüren güçlü araçlar var. Peki, bu verinin "boyutunu" nasıl ölçeriz? Bir veri noktasının orijinden ne kadar "uzak" olduğunu nasıl ifade ederiz? Veya iki farklı veri noktasının birbirine ne kadar "yakın" ya da "uzak" olduğunu nasıl anlarız?

Bu sorular, yapay zekanın en temel görevlerinden olan sınıflandırma, kümeleme ve hata hesaplama gibi işlemlerin kalbinde yatar. Bu soruları cevaplamak için kullandığımız iki temel matematiksel enstrüman vardır: Norm ve Mesafe. Tıpkı bir mimarın cetveli veya bir terzinin mezurası gibi, bu iki kavram da bizim sayısal dünyadaki ölçüm sistemimizi oluşturur.

Norm: Bir Vektörün Öz Büyüklüğü

Bir norm, en basit tanımıyla, bir vektöre "uzunluk" veya "büyüklük" değeri atayan bir fonksiyondur. Bir $\upsilon$ vektörünün normu, genellikle $\|\upsilon\|$ sembolüyle gösterilir. Kısacası "norm", tek bir vektörün orijine göre olan büyüklüğünü ölçen bir cetveldir.

Mesafe: İki Nokta Arasındaki Uzaklık

Mesafe, iki nokta arasındaki "uzaklığı" ölçen bir fonksiyondur. $P_1 ve P_2$ gibi iki nokta arasındaki mesafeyi genellikle $d(P_1, P_2)$ ile gösteririz. İki nokta arasındaki mesafe, o iki noktayı birleştiren fark vektörünün normuna eşittir. Matematiksel olarak bu zarif ilişkiyi şöyle ifade ederiz:

$$ \begin{aligned} & d(P_1, P_2) = \|P_1 - P_2\| \\ \end{aligned} $$

Özetle bir "mesafe" hesaplamak istediğimizde, aslında önce o iki noktadan bir "vektör" oluştururuz ve sonra o vektörün "normunu" alırız.

Norm, bir ölçüm aracıdır (cetvel).
Mesafe, o aracın iki nokta arasında kullanılmasının sonucudur (ölçüm eylemi).

L² Normu (Öklid Normu)

L² normu, ya da diğer adıyla öklid normu, vektörün başlangıcından bitişine kuş uçuşu boyunu tasvir eder. Mantığı en kolay kavranan norm çeşididir. Vektörün bileşenlerinin karelerinin toplamının karekökü alınarak bulunur.

Aşağıda iki boyutlu düzlemdeki bir vektörün öklid normunun hesaplanışını görüyoruz.

$$ \begin{aligned} & \upsilon_1 = [3, 4] \\ \\ & \|\upsilon_1\| = \sqrt{3^2 + 4^2} = 5 \\ \end{aligned} $$

Aşağıda ise üç boyutlu uzaydaki bir vektörün öklid normunun hesaplanışını görüyoruz.

$$ \begin{aligned} & \upsilon_1 = [3, 4, 2] \\ \\ & \|\upsilon_1\| = \sqrt{3^2 + 4^2 + 2^2} = \sqrt{29} \\ \end{aligned} $$

Kağıt üzerinde çizemesek de 3'den fazla boyutlu evrenlerin vektörleri de aynı formüle göre hesaplanır. Örneğin aşağıda beş boyutlu bir evrendeki vektörün öklid normunun hesaplanışını görüyoruz.

$$ \begin{aligned} & \upsilon_1 = [4, 3, 2, 6, 5] \\ \\ & \|\upsilon_1\| = \sqrt{4^2 + 3^2 + 2^2 + 6^2 + 5^2} = 3\sqrt{10} \\ \end{aligned} $$

L² Mesafesi (Öklid Mesafesi)

L² mesafesi, ya da diğer adıyla öklid mesafesi, iki nokta arasındaki kuş uçuşu mesafeyi tasvir eder. Yine mantığı en kolay kavranan mesafe çeşididir. Noktaların arasına bir vektör çizerek, bu vektörün öklid normu hesap edilerek bulunur.

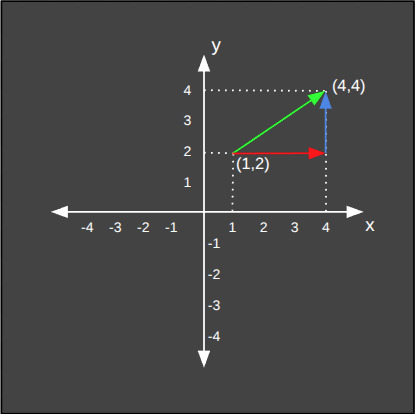
Aşağıda iki boyutlu düzlemdeki bir vektörün öklid mesafesinin hesaplanışını görüyoruz.

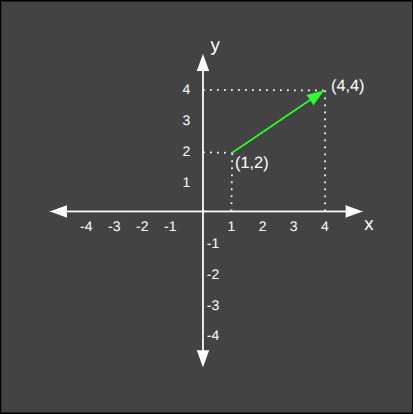
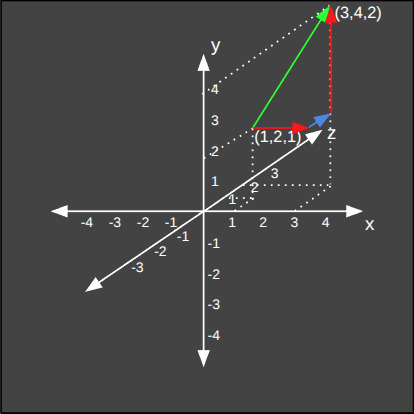
$$ \begin{aligned} & P_1 = (1,2) \\ & P_2 = (4,4) \\ \\ & \upsilon_1 = P_2 - P_1 = [4-1, 4-2] = [3, 2] \\ \\ & \|\upsilon_1\|_2 = \sqrt{3^2 + 2^2} = \sqrt{13} \\ \end{aligned} $$

Aşağıda ise üç boyutlu uzaydaki iki nokta arasındaki öklid mesafesinin hesaplanışını görüyoruz.

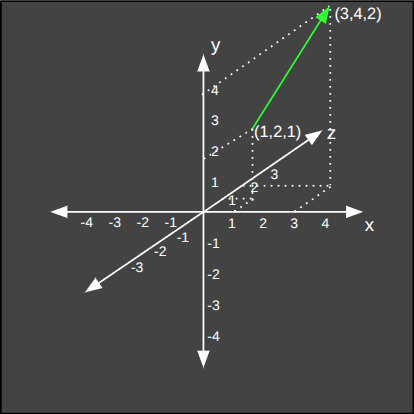
$$ \begin{aligned} & P_1 = (1,2,1) \\ & P_2 = (3,4,2) \\ \\ & \upsilon_1 = P_2 - P_1 = [3-1, 4-2, 2-1] = [2, 2, 1] \\ \\ & \|\upsilon_1\|_2 = \sqrt{2^2 + 2^2 + 1^2} = 3 \\ \end{aligned} $$

Yine kağıt üzerinde çizemesek de 3'den fazla boyutlu evrenlerin mesafeleri de aynı formüle göre hesaplanır. Örneğin aşağıda beş boyutlu bir evrendeki iki nokta arasındaki öklid mesafesinin hesaplanışını görüyoruz.

$$ \begin{aligned} & P_1 = (1,2,1,3,3) \\ & P_2 = (3,4,2,5,1) \\ \\ & \upsilon_1 = P_2 - P_1 = [3-1, 4-2, 2-1, 5-3, 1-3] = [2, 2, 1, 2, -2] \\ \\ & \|\upsilon_1\|_2 = \sqrt{2^2 + 2^2 + 1^2 + 2^2 + (-2)^2} = \sqrt{17} \\ \end{aligned} $$

Öklid mesafesi, KNN, K-Means Clustering, SVM, Hierarchical Clustering ve Distance-Based Anomaly Detection gibi pek çok makine öğrenimi algoritmasında kullanılır.

L¹ Normu (Manhattan Normu)

L¹ Normu, ya da diğer adıyla Manhattan normu, adını ızgara şeklindeki caddelere sahip olan Manhattan'dan almıştır. Bu normda kuş uçuşu doğrusal bir yoldan ziyade, bir taksinin Manhattan caddelerinde gidişi gibi sadece bileşenlerin eksenleri boyunca hareket etmesine izin vardır (x ekseni boyunca 3 birim, y ekseni boyunca 4 birim). Dolayısıyla normun değeri, bileşenlerin mutlak değerlerinin toplamına eşittir.

Aşağıda iki boyutlu düzlemdeki bir vektörün Manhattan normunun hesaplanışını görüyoruz.

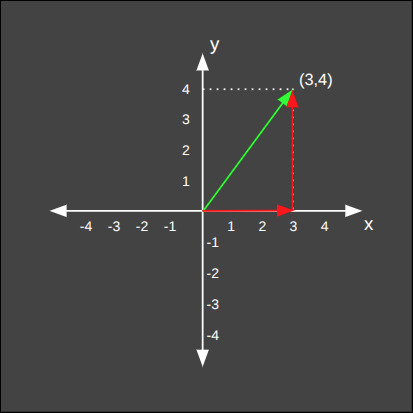
$$ \begin{aligned} & \upsilon_1 = [3, 4] \\ \\ & \|\upsilon_1\|_1 = |3| + |4| = 7 \\ \end{aligned} $$

Aşağıda ise üç boyutlu uzaydaki bir vektörün Manhattan normunun hesaplanışını görüyoruz.

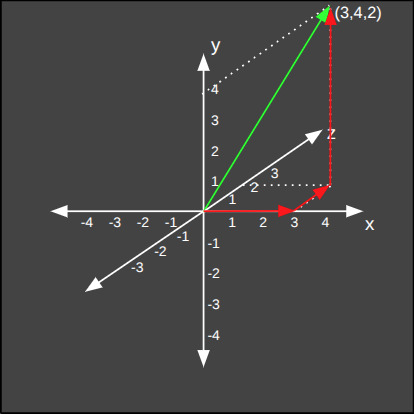
$$ \begin{aligned} & \upsilon_1 = [3, 4, 2] \\ \\ & \|\upsilon_1\|_1 = |3| + |4| + |2| = 9 \\ \end{aligned} $$

3'den fazla boyutlu evrenlerin vektörleri de aynı formüle göre hesaplanır. Aşağıda beş boyutlu bir evrendeki vektörün Manhattan normunun hesaplanışını görüyoruz.

$$ \begin{aligned} & \upsilon_1 = [4, 3, 2, 6, 5] \\ \\ & \|\upsilon_1\|_1 = |4| + |3| + |2| + |6| + |5| = 20 \\ \end{aligned} $$

L¹ Mesafesi (Manhattan Mesafesi)

L¹ mesafesi, ya da diğer adıyla Manhattan mesafesi, iki nokta arasındaki eksenler boyunca mesafeyi tasvir eder. Noktaların arasına bir vektör çizerek, bu vektörün Manhattan normu hesap edilerek bulunur.

Aşağıda iki boyutlu düzlemdeki bir vektörün Manhattan mesafesinin hesaplanışını görüyoruz.

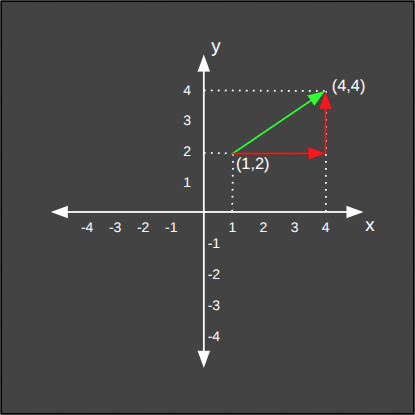
$$ \begin{aligned} & P_1 = (1,2) \\ & P_2 = (4,4) \\ \\ & \upsilon_1 = P_2 - P_1 = [4-1, 4-2] = [3, 2] \\ \\ & \|\upsilon_1\|_1 = |3| + |2| = 5 \\ \end{aligned} $$

Aşağıda üç boyutlu uzaydaki iki nokta arasındaki Manhattan mesafesinin hesaplanışını görüyoruz.

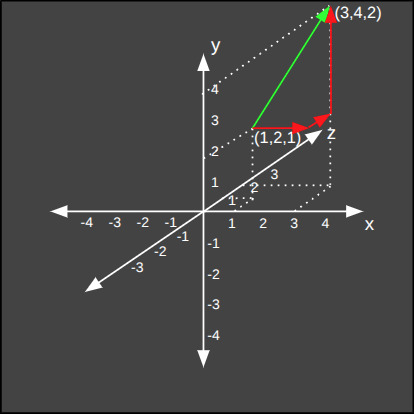
$$ \begin{aligned} & P_1 = (1,2,1) \\ & P_2 = (3,4,2) \\ \\ & \upsilon_1 = P_2 - P_1 = [3-1, 4-2, 2-1] = [2, 2, 1] \\ \\ & \|\upsilon_1\|_1 = |2| + |2| + |1| = 5 \\ \end{aligned} $$

3'den fazla boyutlu evrenlerin mesafeleri de aynı formüle göre hesaplanır. Aşağıda beş boyutlu bir evrendeki iki nokta arasındaki Manhattan mesafesinin hesaplanışını görüyoruz.

$$ \begin{aligned} & P_1 = (1,2,1,3,3) \\ & P_2 = (3,4,2,5,1) \\ \\ & \upsilon_1 = P_2 - P_1 = [3-1, 4-2, 2-1, 5-3, 1-3] = [2, 2, 1, 2, -2] \\ \\ & \|\upsilon_1\|_1 = |2| + |2| + |1| + |2| + |-2| = 9 \\ \end{aligned} $$

Manhattan mesafesi, metin analizi, belge karşılaştırma, bilgisayarlı görü (computer vision) ve görüntü işleme gibi özelliklerinin birbirine dönüşemediği veya sadece yatay/dikey eksenlerde hareketin anlamlı olduğu durumlarda sıkça kullanılır.

L-Sonsuz Normu (Chebyshev Normu)

L-Sonsuz Normu, ya da diğer adıyla Chebyshev normu, vektörün bileşenlerinin mutlak değerlerinin maksimum olanının değerine eşittir.

Böyle bir norma neden ihtiyacımız olabileceğini bir sonraki başlıkta işliyoruz.

Aşağıda iki boyutlu düzlemdeki bir vektörün Chebyshev normunun hesaplanışını görüyoruz.

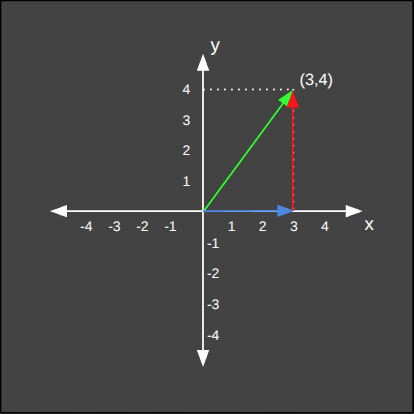
$$ \begin{aligned} & \upsilon_1 = [3, 4] \\ \\ & \|\upsilon_1\|_\infin = max(|3|,|4|) = 4 \\ \end{aligned} $$

Aşağıda ise üç boyutlu uzaydaki bir vektörün Chebyshev normunun hesaplanışını görüyoruz.

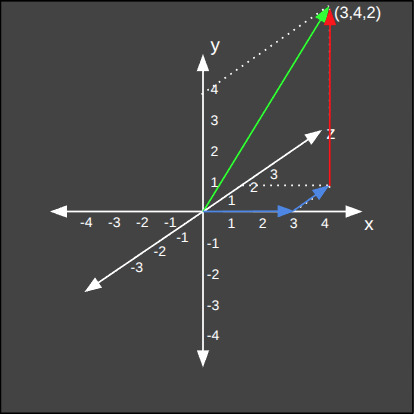
$$ \begin{aligned} & \upsilon_1 = [3, 4, 2] \\ \\ & \|\upsilon_1\|_\infin = max(|3|, |4|, |2|) = 4 \\ \end{aligned} $$

3'den fazla boyutlu evrenlerin vektörleri de aynı formüle göre hesaplanır. Aşağıda beş boyutlu bir evrendeki vektörün Chebyshev normunun hesaplanışını görüyoruz.

$$ \begin{aligned} & \upsilon_1 = [4, 3, 2, 6, 5] \\ \\ & \|\upsilon_1\|_\infin = max(|4|, |3|, |2|, |6|, |5|) = 6 \\ \end{aligned} $$

L-Sonsuz Mesafesi (Chebyshev Mesafesi)

Hesaplanması çok kolay olan Chebyshev normunu gördük ancak böyle bir norma neden ihtiyacımız olabileceğini bir örnek üzerinden işleyelim. Depoda çalışan bir tavan vincini hayal edelim. Bu vinç X ve Y eksenlerinde aynı anda hareket edebilir. Vincin, A(2, 1) noktasından B(9, 5) noktasına bir paket taşıması gerekiyor. Fark Vektörü: (9-2, 5-1) = (7, 4). Vincin X ekseninde 7 birim, Y ekseninde 4 birim hareket etmesi lazım. Vinç, iki motorunu da aynı anda çalıştırır. Y eksenindeki 4 birimlik hareketini tamamladığında, X eksenindeki motor hala çalışıyor olacaktır. Toplam operasyon süresini, daha uzun olan X eksenindeki hareket belirler. Hareketin tamamlanması için gereken süre, max(7, 4) = 7 birim zamandır. İşte bu, Chebyshev mesafesidir.

Aşağıda iki boyutlu düzlemdeki iki nokta arasındaki Chebyshev mesafesinin hesaplanışını görüyoruz.

$$ \begin{aligned} & P_1 = (1,2) \\ & P_2 = (4,4) \\ \\ & \upsilon_1 = P_2 - P_1 = [4-1, 4-2] = [3, 2] \\ \\ & \|\upsilon_1\|_\infin = max(|3|, |2|) = 3 \\ \end{aligned} $$

Aşağıda ise üç boyutlu uzaydaki iki nokta arasındaki Chebyshev mesafesinin hesaplanışını görüyoruz.

$$ \begin{aligned} & P_1 = (1,2,1) \\ & P_2 = (3,4,2) \\ \\ & \upsilon_1 = P_2 - P_1 = [3-1, 4-2, 2-1] = [2, 2, 1] \\ \\ & \|\upsilon_1\|_\infin = max(|2|, |2|, |1|) = 2 \\ \end{aligned} $$

3'den fazla boyutlu evrenlerin mesafeleri de aynı formüle göre hesaplanır. Aşağıda beş boyutlu bir evrendeki iki nokta arasındaki Chebyshev mesafesinin hesaplanışını görüyoruz.

$$ \begin{aligned} & P_1 = (1,2,1,3,3) \\ & P_2 = (3,4,2,5,1) \\ \\ & \upsilon_1 = P_2 - P_1 = [3-1, 4-2, 2-1, 5-3, 1-3] = [2, 2, 1, 2, -2] \\ \\ & \|\upsilon_1\|_\infin = max(|2|, |2|, |1|, |2|, |-2|) = 2 \\ \end{aligned} $$

Chebyshev mesafesi, iki nokta arasındaki etkileşimin en yavaş veya en baskın olan tek bir boyut tarafından belirlendiği, özellikle lojistik ve robotik gibi "darboğaz" (bottleneck) senaryolarında kritik rol oynar.

Sonuç: Veriye Uygun Ölçütü Seçmek

Bu makalede incelediğimiz gibi, "uzaklık" kavramı tek bir formülle sınırlı değildir. L², L¹ ve L-Sonsuz aileleri, bize veri noktaları arasındaki ilişkiyi ölçmek için her biri farklı varsayımlara ve sonuçlara sahip üç temel araç sunar.

L² (Öklid): Boyutlar arası en kısa, 'hipotenüs' yolu. Düşük boyutlu, geometrik olarak sezgisel veriler (örn: KNN, K-Means).
L¹ (Manhattan): Boyutlar boyunca alınan mutlak adımların toplamı. Yüksek boyutlu veriler, ızgara yapılı problemler (örn: Metin analizi, görüntü işleme).
L∞ (Chebyshev): Boyutlar arasındaki en büyük tekil fark. Darboğaz analizi, eş zamanlı sistemler.

Bir makine öğrenmesi modelinde bu ölçütlerden hangisinin seçileceği, modelin hangi veri noktalarını "benzer" veya "yakın" olarak kabul edeceğini temelden belirler ve dolayısıyla modelin doğruluğu ve performansı üzerinde doğrudan bir etkiye sahiptir. Varsayılan olarak sıkça kullanılan Öklid mesafesi her zaman en iyi seçenek olmayabilir. Özellikle yüksek boyutlu verilerle çalışırken Manhattan mesafesinin sağlamlığı veya bir sistemdeki maksimum hatayı tespit etmeye çalışırken Chebyshev mesafesinin yeteneği kritik avantajlar sunabilir.

Zamanı geldiğinde bu ve buna benzer pek çok aracı kullanacağız. Şimdilik matematiksel temellerimizi sağlamlaştırmaya devam edelim.

Yazar: Levent KARAGÖL