Matrisler, yapay zekanın vektörlerle temsil edilen veriyi dönüştürmesini, işlemesini ve aralarındaki karmaşık ilişkileri modellemesini sağlayan temel operatörlerdir. Bu makalede, matrislerin tanımını, temel cebirsel operasyonlarını, en kritik görevi olan matris çarpımını ve tersini alma ile determinant gibi ileri düzey kavramlarını yapay zeka perspektifiyle inceleyeceğiz.

Matris Nedir?

Yine basit bir tanımla başlayalım. Programcı gözüyle matris, içerisinde sayısal değerler barındıran iki boyutlu bir dizidir. Matematiksel ve geometrik açıdan ise matris, tek bir nesne olmaktan çok, bir dönüşümün (transformation) ta kendisidir. Onu, uzaydaki tüm vektörlere ne yapılacağını söyleyen bir 'kural seti' olarak düşünebiliriz. Bu makale bittiğinde, 3 boyutlu uzaydaki bir vektörü istediğimiz gibi döndürebilecek, boyutunu büyütebilecek, şeklini değiştirebilecek, bunları toplu olarak bir kerede gerçekleştirebilecek veya geri alabileceğiz.

Ama öncesinde matrisi en temel hali ile ele alalım. Aşağıda 3x4 boyutunda bir matris yer almaktadır.

Elbette sadece bu şekle bakarak ne olduğunu anlamak pek mümkün değil. Bu matris 3 satırdan oluşuyor ve her satırında 4 adet özellik bulunuyor. Bu haliyle 3 farklı sensörden alınan 4 farklı değer de olabilir. Ya da 3 farklı şehirdeki son 4 günlük sıcaklık değişimleri de olabilir. Şimdilik tek bildiğimiz, içerisinde 12 adet veri sakladığıdır.

Matrislerde Toplama

İki farklı matrisi toplayabilmemiz için temel şart, matrislerin boyutlarının aynı olmasıdır. Bu oldukça kolay bir işlemdir. Birinci matristeki her eleman, ikinci matriste kendi pozisyonundaki sayı ile toplanarak bileşik matris değeri elde edilir.

Aşağıda 2x3 boyutundaki iki matrisin toplamını görüyoruz.

Matrislerde Skaler Çarpma

Bir matrisi tek bir sayıyla (skaler) çarpmak, matrisin her elemanını bu sayıyla çarpmak anlamına gelir. Aşağıda bu işlemin örneğini görüyoruz.

Matrislerin Çarpımı

Burası işlerin ilginçleştiği yer ve bundan sonra dönüşüm için bol miktarda yapacağımız işlemin ta kendisi. İki matrisi çarpabilmek için temel şart, birinci matrisin sütun sayısı, ikinci matrisin satır sayısına eşit olmasıdır. Örneğin 3x4 ve 4x2 boyutlarındaki iki matris birbirleriyle çarpılabilir. Ancak 3x4 ve 3x4 boyutlarındaki iki matris birbirleriyle çarpılamaz.

Matris çarpım işleminde, birinci matrisin satır vektörleri ile ikinci matrisin sütun vektörleri arasında sırayla nokta çarpım (Dot Product) uygulanır (Vektörlerde nokta çarpım konusunu bir önceki makalemizde işlemiştik). (m x n) matrisi ile bir (n x p) matrisi çarpıldığında, sonuç (m x p) boyutunda yeni bir matris olur.

Bu işlemi bir örnek üzerinde görelim.

Determinant Hesabı

Bir matrisin determinantını almak için yapılması gerekenler, matrisin boyutuna göre değişiklik gösterir. Aşağıda 2x2 bir matrisin determinantının alınmasını görüyoruz. Burada çapraz sayılar birbirleri ile çarpılıp sonuçlar birbirinden çıkartılarak determinant hesabı yapılır.

Aşağıda ise 3x3 bir matrisin determinantının alınmasını görüyoruz. Bu matrisin determinantını almak için 1. satırdaki 3 eleman ile, bunların bulunduğu satır ve sütundaki elemanlar kapatılarak elde edilen 2x2 matrislerin determinantları çarpılıp aşağıdaki işleme tabii tutulur.

Matrisin Tersini Almak

Kompleks olmaması adına 2x2'lik matrisin tersini almayı işleyeceğiz. Bir matrisin tersinin alınabilmesi için öncelikle determinantının 0'dan farklı olduğunun teyit edilmesi gerekir. Determinantı 0 olan matrislerin tersi yoktur.

Determinantı 0'dan farklı olan 2x2 matrisler için ters işleminde, 1. ve 4. elemanın yeri değiştirilir. Ardından 2. ve 3. elemanın işareti değiştirilir. Son olarak ortaya çıkan matris determinanta bölünür. Aşağıda bu işlemin örneğini görüyoruz

Birim Matris

Şu andan itibaren matrisleri kullanarak vektörlerde çeşitli modifikasyonlar yapacağız. En basit matris olan birim matris ile başlıyoruz. Bu matris aslında çarpma işlemindeki 1 sayısına denk gelen matris türüdür. Kendisi ile çarpılan vektörde hiçbir değişiklik yapmaz. Birim matris aşağıdaki şekilde gösterilir.

Bu matrisi hemen bir vektör ile çarparak sonucu inceleyelim.

$$ \begin{aligned} & \upsilon_1 = \begin{bmatrix} 4 \\ 3 \\ \end{bmatrix} \\ \space \\ & A = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \\ \space \\ & A . \upsilon_1 = \begin{bmatrix} (1.4 + 0.3) \\ (0.4 + 1.3) \\ \end{bmatrix} = \begin{bmatrix} 4 \\ 3 \\ \end{bmatrix} = \upsilon_1 \end{aligned} $$

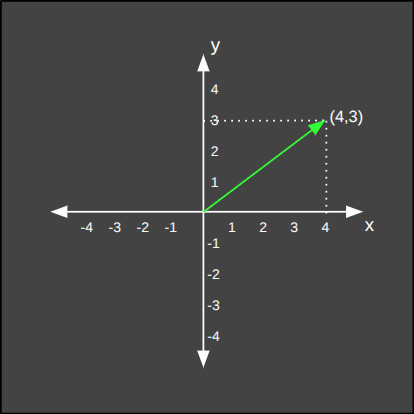
Boyutlandırma Matrisi

Bu matris, çarpıldığı vektörün boyutunu değiştirir. Eşit oranlı ve farklı oranlı büyütme/küçültme için farklı değerler kullanılabilir. Örneğin aşağıda çarpıldığı vektörü iki katına çıkartan bir matris örneği görüyoruz.

$$ \begin{aligned} & \upsilon_1 = \begin{bmatrix} 1 \\ 2 \\ \end{bmatrix} \\ \space \\ & A = \begin{bmatrix} 2 & 0 \\ 0 & 2 \\ \end{bmatrix} \\ \space \\ & A . \upsilon_1 = \begin{bmatrix} (2.1 + 0.2) \\ (0.1 + 2.2) \\ \end{bmatrix} = \begin{bmatrix} 2 \\ 4 \\ \end{bmatrix} = 2.\upsilon_1 \end{aligned} $$

Aşağıda ise çarpıldığı vektörü yarı yarıya küçülten bir matris örneği görüyoruz.

$$ \begin{aligned} & \upsilon_1 = \begin{bmatrix} 2 \\ 4 \\ \end{bmatrix} \\ \space \\ & A = \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \\ \end{bmatrix} \\ \space \\ & A . \upsilon_1 = \begin{bmatrix} (0.5.2 + 0.4) \\ (0.2 + 0.5.4) \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \\ \end{bmatrix} = 0.5.\upsilon_1 \end{aligned} $$

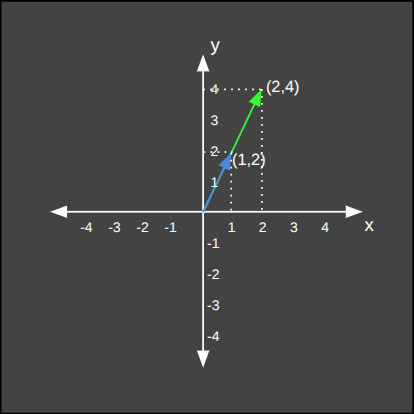
Aşağıda da çarpıldığı vektörü farklı en/boy oranında büyüten, yani şeklini değiştiren bir matris örneği görüyoruz.

$$ \begin{aligned} & \upsilon_1 = \begin{bmatrix} 1 \\ 2 \\ \end{bmatrix} \\ \space \\ & A = \begin{bmatrix} 3 & 0 \\ 0 & 2 \\ \end{bmatrix} \\ \space \\ & A . \upsilon_1 = \begin{bmatrix} (3.1 + 0.2) \\ (0.1 + 2.2) \\ \end{bmatrix} = \begin{bmatrix} 3 \\ 4 \\ \end{bmatrix} \end{aligned} $$

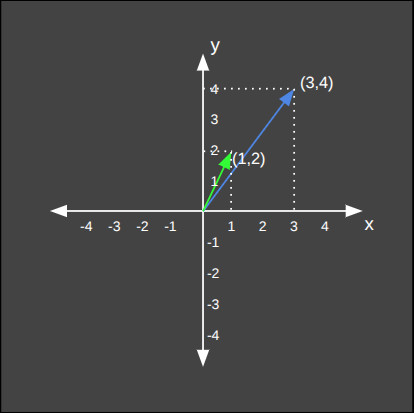
Döndürme Matrisi

Bu matris, çarpıldığı vektörü saat yönünün tersine \(\theta\) açısı kadar döndürür. Vektörün yazılışı aşağıdaki gibidir.

Aşağıdaki örnekte vektörümüzü saat yönünün tersine 60 derece çeviriyoruz.

$$ \begin{aligned} & \upsilon_1 = \begin{bmatrix} 2 \\ 2 \\ \end{bmatrix} \\ \space \\ & A = \begin{bmatrix} cos(60) & −sin(60) \\ sin(60) & cos(60) \\ \end{bmatrix} = \begin{bmatrix} 0.5 & -0.866 \\ 0.866 & 0.5 \\ \end{bmatrix} \\ \space \\ & A . \upsilon_1 = \begin{bmatrix} (0.5.2 + (-0.866).2) \\ (0.866.2 + 0.5.2) \\ \end{bmatrix} = \begin{bmatrix} -0.732 \\ 2.732 \\ \end{bmatrix} \end{aligned} $$

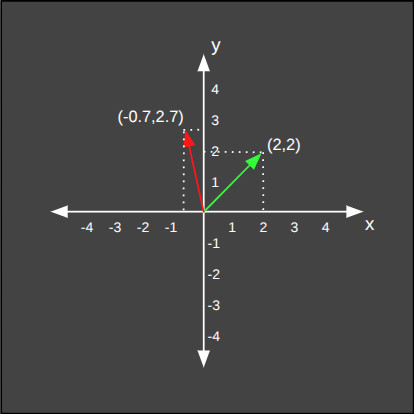
Değişikliği Geri Alma

Bir vektör ile çarpılan bir matris sonucunda vektörde yapılan değişiklikleri geri almak istersek, çarpılan matrisin tersi ile vektörü tekrar çarpmamız gerekir. Bunu bir çeşit "undo" işlemi olarak düşünebiliriz.

Bu işlemi hemen bir örnek üzerinden tecrübe edelim. Bir vektörü saatin ters yönünde 90 derece döndürecek bir matris çarpımı yapalım. Ardından bu matrisin tersi ile çarparak orjinal yerine döndüğünü teyit edelim.

$$ \begin{aligned} & \upsilon_1 = \begin{bmatrix} 2 \\ 2 \\ \end{bmatrix} \\ \space \\ & A = \begin{bmatrix} cos(90) & −sin(90) \\ sin(90) & cos(90) \\ \end{bmatrix} = \begin{bmatrix} 0 & -1 \\ 1 & 0 \\ \end{bmatrix} \\ \space \\ & A . \upsilon_1 = \begin{bmatrix} (0.2 + (-1).2) \\ (1.2 + 0.2) \\ \end{bmatrix} = \begin{bmatrix} -2 \\ 2 \\ \end{bmatrix} \end{aligned} $$

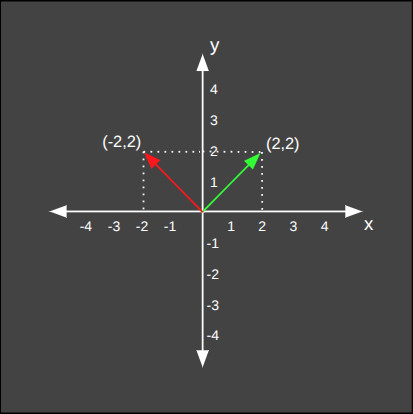
Vektörümüzü saat yönünün tersi yönünde 90 derece çevirdik. Şimdi sıra geldi döndürme matrisinin tersini bulmaya.

Son olarak ters matrisi vektörümüz ile çarpıyoruz.

$$ \begin{aligned} & \upsilon_1 = \begin{bmatrix} -2 \\ 2 \\ \end{bmatrix} \\ \space \\ & A = \begin{bmatrix} 0 & 1 \\ -1 & 0 \\ \end{bmatrix} \\ \space \\ & A . \upsilon_1 = \begin{bmatrix} (0.(-2) + 1.2) \\ (-1.(-2) + 0.2) \\ \end{bmatrix} = \begin{bmatrix} 2 \\ 2 \\ \end{bmatrix} \end{aligned} $$

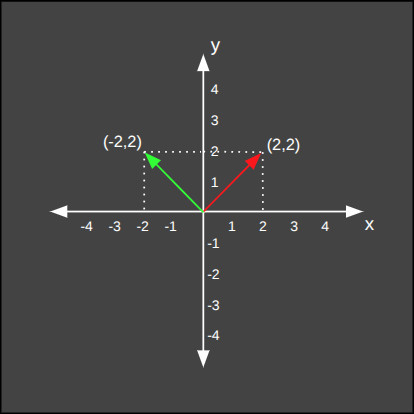
İşlem Birleştirme

Bir vektöre arka arkaya birden fazla matris işlemi gerçekleştirilecekse, değişiklik matrisleri birbirleri ile çarpılarak ortaya çıkan matris bir kerede vektör ile çarpılabilir. Bu işlemin sonucu, matrisleri tek tek çarpmakla aynıdır.

Bu işlemi bir örnek üzerinde görelim. Vektörümüze öncelikle ayrı ayrı döndürme ve büyütme işlemleri uygulayalım. Ardından aynı işlemi, iki matrisi birbiri ile çarptıktan sonra toplu olarak yapalım ve iki sonucun eşit olduğunu teyit edelim. Öncelikle ayrı ayrı işlem yapıyoruz.

$$ \begin{aligned} & \upsilon_1 = \begin{bmatrix} 1 \\ 2 \\ \end{bmatrix} \\ \space \\ & A = \begin{bmatrix} 2 & 0 \\ 0 & 2 \\ \end{bmatrix} \\ \space \\ & A . \upsilon_1 = \begin{bmatrix} (2.1 + 0.2) \\ (0.1 + 2.2) \\ \end{bmatrix} = \begin{bmatrix} 2 \\ 4 \\ \end{bmatrix} = \upsilon_2 \\ \space \\ & B = \begin{bmatrix} cos(90) & −sin(90) \\ sin(90) & cos(90) \\ \end{bmatrix} = \begin{bmatrix} 0 & -1 \\ 1 & 0 \\ \end{bmatrix} \\ \space \\ & B . \upsilon_2 = \begin{bmatrix} (0.2 + (-1).4) \\ (1.2 + 0.4) \\ \end{bmatrix} = \begin{bmatrix} -4 \\ 2 \\ \end{bmatrix} \end{aligned} $$

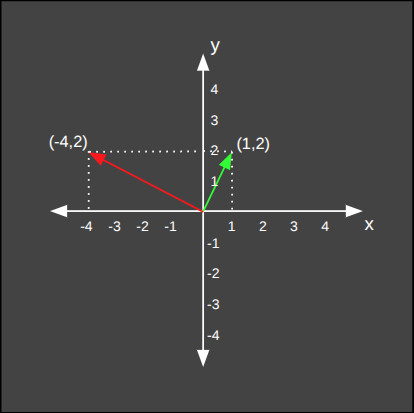
Şimdi de öncelikle iki dönüşüm matrisini çarpıp tek bir dönüşüm matrisi oluşturacak ve ardından bu matris ile vektör üzerinde işlem yapacağız.

$$ \begin{aligned} & \upsilon_1 = \begin{bmatrix} 1 \\ 2 \\ \end{bmatrix} \\ \space \\ & A = \begin{bmatrix} 2 & 0 \\ 0 & 2 \\ \end{bmatrix} \\ \space \\ & B = \begin{bmatrix} cos(90) & −sin(90) \\ sin(90) & cos(90) \\ \end{bmatrix} = \begin{bmatrix} 0 & -1 \\ 1 & 0 \\ \end{bmatrix} \\ \space \\ & A . B = \begin{bmatrix} (2.0 + 0.1) & (2.(-1) + 0.0) \\ (0.0 + 2.1) & (0.(-1) + 2.0) \\ \end{bmatrix} = \begin{bmatrix} 0 & -2 \\ 2 & 0 \\ \end{bmatrix} = C \\ \space \\ & C . \upsilon_1 = \begin{bmatrix} (0.1 + (-2).2) \\ (2.1 + 0.2) \\ \end{bmatrix} = \begin{bmatrix} -4 \\ 2 \\ \end{bmatrix} \end{aligned} $$

Örnekte de gördüğümüz üzere aynı sonuca ulaştık. Tek bir vektör ile işlem yaptığımız için iki örnek arasında bir performans farkı yoktu ancak çok sayıda vektör üzerinde işlem yapacak olsaydık, işlem sayısı yarıya düşmüş olacaktı.

Matrisler ve Yapay Zeka

Böylece matrisler makalemizin de sonuna gelmiş olduk. Burada görük ki, matrisler sadece içerisinde sayı saklamaktan sorumlu veri yapıları değil, aynı zamanda özel matrislerin verilerle çarpımı sonucunda, bu verilerde istediğimiz değişikliğe sebep olan birer operatör olarak da kullanılabiliyor. Bu operatörler, yapay sinir ağlarında ve modern yapay zekanın tamamında çok önemli görevler üstlenirler.

• Yapay Sinir Ağlarının Çekirdeğinde: Bir sinir ağının katmanları arasındaki bağlantıların gücünü temsil eden ağırlıklar (weights), devasa matrisler halinde saklanır. Ağın "öğrenme" süreci, temelde bu matrislerdeki sayıların doğru değerlere ayarlanmasıdır. Bir verinin ağ içindeki yolculuğu, devasa matris çarpımlarından geçer.
• Bilgisayarlı Görüde (Computer Vision): Baktığımız her dijital fotoğraf, piksellerin parlaklık değerlerinden oluşan bir matristir. Yapay zekanın bir görüntüdeki nesneleri tanıması, kenarları veya dokuları tespit etmesi, bu pikseller matrisine uygulanan bir dizi karmaşık matris operasyonu (filtreleme, konvolüsyon vb.) sayesinde mümkün olur.
• Doğal Dil İşlemede (NLP): Kullandığımız kelimelerin anlamları bile, anlamsal ilişkilerini koruyan vektörler olarak dev "gömme (embedding)" matrislerinde saklanır. ChatGPT gibi gelişmiş dil modellerinin temelindeki "Attention" mekanizması, bir cümlenin anlamını çıkarmak için kelimeler arasındaki ilişki skorlarını hesaplayan sofistike matris işlemleri üzerine kuruludur.
• Öneri Sistemlerinde (Recommender Systems): Milyonlarca kullanıcının binlerce ürüne verdiği puanlar, dev bir "kullanıcı-ürün" matrisi olarak temsil edilir. Yapay zeka, bu matristeki boşlukları doldurarak size bir sonraki favori filminizi veya şarkınızı önerir.

Zamanı geldiğinde biz de bu araçları kullanıyor olacağız. Şimdilik matematiksel temellerimizi kurmaya devam edelim.

Yazar: Levent KARAGÖL