1. Vektörler

10 Ekim 2025

6 dakika

101 görüntüleme

Vektörler, yapay zeka ve makine öğrenmesinde verinin sayısal temsilinin temelini oluşturur. Makalemizde, bu temel matematiksel yapıların tanımı, toplama, skaler çarpma, nokta çarpma gibi temel cebirsel operasyonları ve vektörlerde benzerlik konularını inceleyeceğiz.

Vektör Nedir?

Basit bir tanım ile başlayalım. Programcı gözüyle bakıldığında vektör, içerisinde birden fazla sayısal değer saklayabilen tek boyutlu bir dizidir. Fizik ve geometride vektör ise, hem büyüklüğü (magnitude) hem de yönü (direction) olan bir nesnedir. Onu, uzayda bir noktadan diğerine giden bir ok ($\upsilon$) olarak hayal edebiliriz. Bir geminin rotası (hız ve yön) veya bir nesneye uygulanan kuvvet mükemmel birer vektör örneğidir.

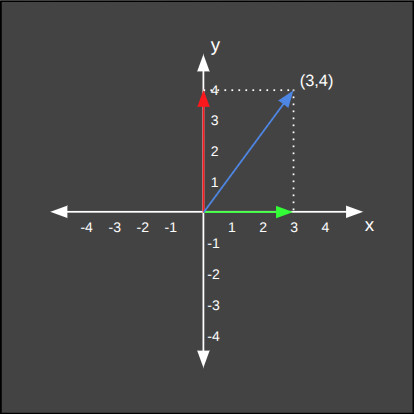
İki boyutlu bir düzlemde yer alan iki adet vektörü ele alalım. Bunların matematiksel olarak yazılışı ve iki boyutlu koordinat sisteminde gösterilişi aşağıdaki gibidir.

$$ \begin{aligned} & \upsilon_1 = [3, 4] \\ & \upsilon_2 = [-2, 3] \end{aligned} $$

İki boyutlu düzlemde görüntülediğimiz anda anlaşılıyor ki, basit iki sayı içeren bir vektör aslında hem bir büyüklük, hem de yön bilgisini içeriyor.

Şimdi de üç boyutlu uzayda yer alan iki adet vektörü ele alalım. Bunların matematiksel olarak yazılışı ve üç boyutlu koordinat sisteminde gösterilişi aşağıdaki gibidir.

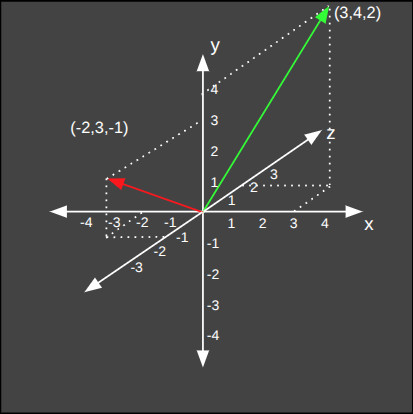
$$ \begin{aligned} & \upsilon_1 = [3, 4, 2] \\ & \upsilon_2 = [-2, 3, -1] \end{aligned} $$

Peki 4, 5 veya 10 elemanı olan bir vektörü nasıl çizerdik? Ne yazık ki 3 boyuttan daha fazla çizimi kağıt üzerinde yapamıyoruz. Ama matematiğin güzelliği de burada. 3 boyutlu bir evrende sıkışmış bizlerin bile 300 boyutlu bir evren hakkında hesaplama yapmasına imkan tanıyor.

Artık vektörün bir sayı dizisinden ibaret olmadığını, bir "büyüklüğünün", bir "yönünün", özetle bir "şeklinin" olduğunu biliyoruz. Bir nesnenin şeklini bilmemiz, başka bir nesne ile karşılaştırmamıza ve benzerliğini hesaplamamıza imkan sağlar. İleride NLP bölümünde göreceğimiz gibi, bu bize "araba" kelimesi ile "otomobil" kelimesinin benzediğini, ancak "kitap" kelimesinin benzemediğini gösterecek. Elbette bunun için öncelikle metinleri sayısal hale getirmeyi, yani "vektörize" etmeyi öğrenmemiz gerekli. Şimdilik bu bilgi aklımızın bir kenarında bulunsun.

Vektörleri Toplama

Matematiksel olarak iki vektörü toplayabilmek için temel şart, iki vektörün aynı miktarda sayıdan oluşmasıdır. Birinci vektördeki her bir sayı, ikinci vektördeki aynı sıradaki sayı ile toplanarak bileşke vektör elde edilir.

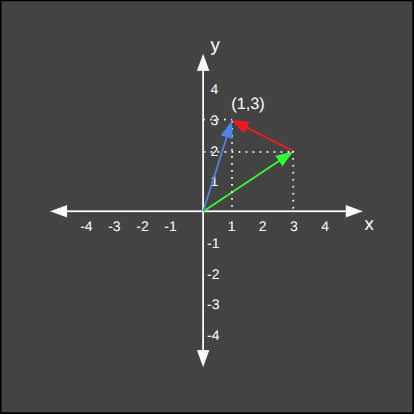
$$ \begin{aligned} & \upsilon_1 = [3, 2] \\ & \upsilon_2 = [-2, 1] \\ & \\ & \upsilon_1 + \upsilon_2 = [3 + (-2), 2 + 1] = [1, 3] \end{aligned} $$

Ortaya çıkan bileşke vektör her iki vektörün "özelliklerinin birleşmesidir". İlerleyen makalelerde göreceğimiz gibi, bu birleşme vektörize edilmiş metinlerde aşağıdaki gibi işlemlerin ve çıkarımların yapılmasına imkan sağlar.

vektör('kral') - vektör('adam') + vektör('kadın') = vektör('kraliçe')

Vektörlerde Skaler Çarpma

Bir vektörü tek bir sayıyla (skaler) çarpmak, vektörün yönünü değiştirmeden büyüklüğünü (uzunluğunu) ölçeklendirir ve bu işleme skaler çarpma adı verilir.

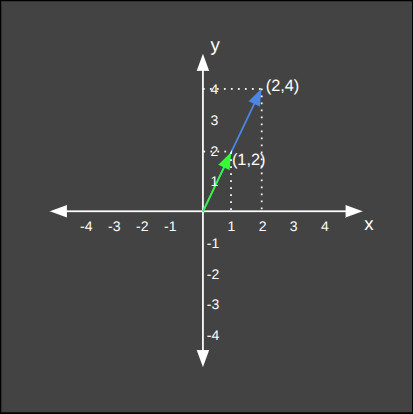
$$ \begin{aligned} & \upsilon_1 = [1, 2] \\ & \upsilon_2 = 2.\upsilon_1 \\ & \\ & \upsilon_2 = [2.1, 2.2] = [2, 4] \end{aligned} $$

Bu basit işlem ile vektörün yönünü değiştirmeden büyüklüğünü değiştirerek daha rahat ölçülebilir hale getirebiliriz.

Makine öğrenmesi modellerinin daha iyi performans göstermesi için özelliklerin değer aralıklarını ayarlamak (normalize etmek) gerekir. Bu işlem skaler çarpma ve toplamayı içerir.

Vektörlerde Uzunluk Hesaplama

Bir vektörü uzunluğunu hesaplamak için bileşenlerinin karesini alıp topladıktan sonra çıkan ifadenin karekökünü alırız. Bu formül ikiden fazla elemanı olan vektörler için de geçerlidir.

$$ \begin{aligned} & \upsilon_1 = [3, 4] \\ \\ & \|\upsilon_1\| = \sqrt{3^2 + 4^2} = 5 \\ \end{aligned} $$

Vektörlerde Nokta Çarpım (Dot Product)

Vektörlerde nokta çarpım (dot product) iki vektörün aynı sıradaki elemanlarının birbiriyle çarpılıp çıkan sonuçların toplanması ile tek bir sayının elde edildiği özel bir işlemdir. Vektörlerin çarpılabilmesi için aynı boyda olması gerekir

$$ \begin{aligned} & \upsilon_1 = [3, 2] \\ & \upsilon_2 = [-2, 1] \\ & \\ & \upsilon_1 . \upsilon_2 = (3 . (-2)) + (2 . 1) = -4 \end{aligned} $$

Vektörlerde nokta çarpım işlemi, bir sonraki başlıkta göreceğimiz gibi iki vektörün birbirine ne kadar benzediğinin hesaplanması için oldukça önemlidir.

Vektörlerde Benzerlik

İki vektörün birbirine ne kadar benzediği hesaplamak için $ benzerlik(\upsilon_1,\upsilon_2) = cos(\theta) = \frac {\upsilon_1.\upsilon_2}{\|\upsilon_1\|.\|\upsilon_2\|} $ formülünden faydalanılır. Bu formül bize -1 ile +1 arasında sonuçlar verir. Buna göre sonuç;

1'e yakınsa: Vektörler çok benzer yöndedir.
0'a yakınsa: Vektörler neredeyse diktir, yani alakasızdır.
-1'e yakınsa: Vektörler zıt yönlerdedir.

Üç farklı vektör çifti için benzerlik hesaplaması yapalım.

$$ \begin{aligned} & \upsilon_1 = [4, 3] \\ & \upsilon_2 = [1, 1] \\ & \\ & \upsilon_1 . \upsilon_2 = (4 . 1) + (3 . 1) = 7 \\ & \\ & \|\upsilon_1\| = \sqrt{4^2 + 3^2} = 5 \\ & \|\upsilon_2\| = \sqrt{1^2 + 1^2} = \sqrt{2} \\ & \\ & benzerlik(\upsilon_1,\upsilon_2) = \frac {7}{5.\sqrt{2}} \approx 0.99 \\ \end{aligned} $$

$$ \begin{aligned} & \upsilon_1 = [4, 3] \\ & \upsilon_2 = [-2, 2] \\ & \\ & \upsilon_1 . \upsilon_2 = (4 . (-2)) + (3 . 2) = -2 \\ & \\ & \|\upsilon_1\| = \sqrt{4^2 + 3^2} = 5 \\ & \|\upsilon_2\| = \sqrt{(-2)^2 + 2^2} = 2\sqrt{2} \\ & \\ & benzerlik(\upsilon_1,\upsilon_2) = \frac {-2}{5.2\sqrt{2}} \approx -0.14 \\ \end{aligned} $$

$$ \begin{aligned} & \upsilon_1 = [4, 3] \\ & \upsilon_2 = [-2, -2] \\ & \\ & \upsilon_1 . \upsilon_2 = (4 . (-2)) + (3 . (-2)) = -14 \\ & \\ & \|\upsilon_1\| = \sqrt{4^2 + 3^2} = 5 \\ & \|\upsilon_2\| = \sqrt{(-2)^2 + (-2)^2} = 2\sqrt{2} \\ & \\ & benzerlik(\upsilon_1,\upsilon_2) = \frac {-14}{5.2\sqrt{2}} \approx -0.99 \\ \end{aligned} $$

Yukarıda gerçekleştirdiğimiz işlemler, ileride "araba" ve "otomobil" kelimelerinin vektörize edilmiş hallerinin benzerliğinin kıyaslanması için gerekli olacak. Şimdilik konunun matematiksel temellerini öğrenmiş ve yapay zeka servüvenimize başlamış olduk.

Yazar: Levent KARAGÖL