8. Trigonometri

19 Ekim 2025

9 dakika

66 görüntüleme

Trigonometri, genellikle geometri ile ilişkilendirilse de, yapay zeka ve veri bilimi alanlarında kritik öneme sahip temel bir matematik dalıdır. Vektörlerin yönünü, verideki periyodik desenleri ve uzamsal dönüşümleri anlamak için gerekli araçları sunar. Bu makalede, trigonometrinin temel prensiplerini ve bu prensiplerin modern yapay zeka sistemlerinde, özellikle vektör benzerlik ölçümleri ve sinir ağı mimarilerinde nasıl uygulandığını inceleyeceğiz.

Dik Üçgen ve Trigonometrik Fonksiyonlar

Trigonometrinin özü, bir dik üçgenin kenarları ve açıları arasındaki ilişkileri tanımlayan üç temel fonksiyona dayanır: Sinüs (sin), Cosinüs (cos) ve Tanjant (tan). Bir $\theta$ açısı için bu fonksiyonlar şu şekilde tanımlanır:

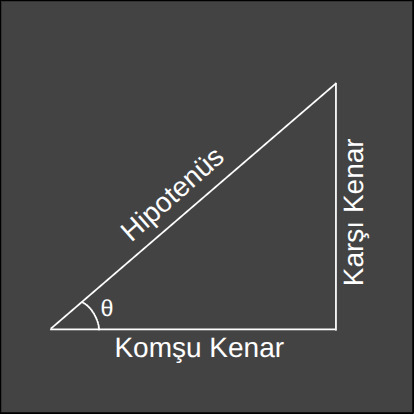
$$ \begin{aligned} & sin(\theta) = \frac{\text{Karşı Kenar}}{\text{Hipotenüs}} \\ \\ & cos(\theta) = \frac{\text{Komşu Kenar}}{\text{Hipotenüs}} \\ \\ & tan(\theta) = \frac{\text{Karşı Kenar}}{\text{Komşu Kenar}} \end{aligned} $$

Bu eşitlikler hem matematikte, hem de fizikte pek çok bilinmezin kapılarını aralar. Bir dik üçgende açıyı ve kenarlardan herhangi birini bilirsek, geri kalanları hesaplamamıza imkan sağlar. Benzer şekilde iki kenarı bildiğimiz durumda da, açıları hesaplamamıza imkan verir.

Peki tüm bunlar, özellikle de yapay zeka için neden önemli? Hatırlarsanız, matematik kategorisindeki makalelere vektörlerle başlamıştık. Yapay zeka için sadece sayılar değil, metinler, sesler, resimler ve videolar da aslında birer vektördür. Eğer vektörlerin koordinatlarını bilirsek, trigonometrik fonksiyonlarla aralarındaki açıyı hesap edebiliriz. Bu da bize iki vektörün birbirine olan benzerliğini verir. Yapay zekanın temeli kıyas ve benzerlik karşılaştırması olduğuna göre, burada trigonometrinin değeri daha da öne çıkar.

Trigonometri ve Birim Çember

Trigonometriden bahsedip de birim çemberi işlemezsek olmaz. Birim çember, herhangi bir $\theta$ açısı için sinüs ve cosinüs değerlerinin değişimini ve birbirleri arasındaki ilişkiyi gösteren çok temel bir araçtır.

Birim çember, analitik düzlemde yarı çapı 1 olan ve merkezi originde bulunan bir çemberdir. Bu çember üzerindeki herhangi bir nokta için, orijinden o noktaya çizilen doğru parçasının x eksenine yaptığı açının sinüs değeri, o noktanın y eksenindeki koordinatıdır. Benzer şekilde, o noktanın x eksenindeki koordinatı da bu açının cosinüs değeridir.

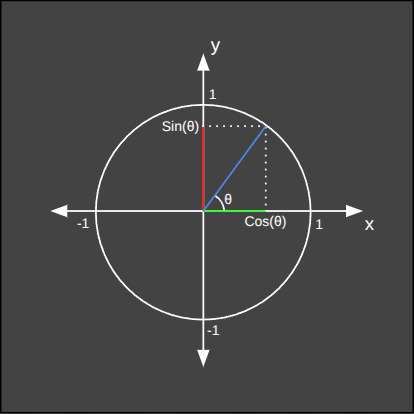
Birim çember, bize trigonometri hakkında pek çok kuralı ve ilişkiyi görsel olarak anlamamıza yardımcı olur.

Sinüs ve Cosinüs değerleri -1 ila +1 arasında değişir
Sinüs ve Cosinüs değerlerinin biri artarken diğeri azalır
Sinüs ve Cosinüs değerleri 360 derecede tamamlanan periyodik bir hareket halindedir

Radyan Cinsinden Açılar

Birim çemberde de gördüğümüz gibi, trigonometrik fonksiyonlar 180 derecede bir tersine döner ve 360 derecede bir kendini tekrarlar. Bu sebeple trigonometrik denklemlerde ve daha sonra göreceğimiz türev ve integralde açılar genellikle radyan cinsinden ifade edilir. Radyan, bir açının ölçüsünü, o açının oluşturduğu yay uzunluğunun yarıçapa oranı olarak tanımlar. Bir tam tur (360 derece) radyan cinsinden $2\pi$ radyandır.

$$ \begin{aligned} & \pi \text{ radyan} = 180^\circ \\ & 2\pi \text{ radyan} = 360^\circ \\ \\ & cos(\pi) = -1 \\ \\ & sin(\frac{\pi}{2}) = 1 \\ \end{aligned} $$

Trigonometrik Dönüşümler

Her ne kadar trigonometrik hesaplamaları bilgisayar bizim adımıza yapacak olsa da, farklı çözümlere kapı araladığı için aşağıdaki dönüşümleri bilmekte fayda var.

$$ \begin{aligned} & tan(\theta) = \frac{sin(\theta)}{cos(\theta)} \\ \\ & sin^2(\theta) + cos^2(\theta) = 1 \\ \\ & sin(2\theta) = 2.sin(\theta).cos(\theta) \\ \\ & cos(2\theta) = cos^2(\theta) - sin^2(\theta) \\ \\ & cos^2(\theta) = \frac{1 + cos(2\theta)}{2} \\ \\ & sin^2(\theta) = \frac{1 - cos(2\theta)}{2} \\ \end{aligned} $$

Trigonometrik Fonksiyon Grafikleri

Sinüs ve Cosinüs fonksiyonları periyodik fonksiyonlardır ve belirli aralıklarla kendilerini tekrarlarlar. Aşağıdaki grafiklerde bu fonksiyonların 0 ile $2\pi$ arasındaki davranışlarını görebiliriz.

Trigonometrik fonksiyonlardaki bu salınım, yapay zeka ve makine öğrenimi modellerinde periyodik desenleri tanımlamamıza imkan sağlar. Özellikle zaman serisi verilerinde, mevsimsel değişiklikleri ve döngüsel kalıpları yakalamak için bu fonksiyonlar kritik öneme sahiptir.

Ters Trigonometrik Fonksiyonlar

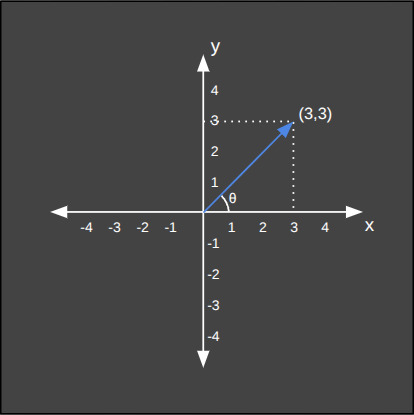
Ters trigonometrik fonksiyonlar, bir açının ölçüsünü bulmamıza yardımcı olur. Yapay zeka uygulamalarında, özellikle vektörlerin yönünü belirlemek ve uzamsal ilişkileri anlamak için kullanılırlar. Bir noktanın kartezyen koordinatlarını $(x, y)$ bildiğimizde, o noktaya olan açıyı $(\theta)$ bulmak için $\arctan(y, x)$ fonksiyonunu kullanırız. Bu, bir robotun hedefe yönelmesi, robot bacakları için ters kinematik (inverse kinematics) hesaplamaları veya bir oyundaki karakterin fare imlecine dönmesi gibi görevlerde kullanılan temel fonksiyondur.

$$ \begin{aligned} & \theta = arctan\left(\frac{y}{x}\right) \\ \\ & \theta = arctan\left(\frac{3}{3}\right) \\ \\ & \theta = arctan(1) = \frac{\pi}{4} \text{ radyan} = 45^\circ \\ \end{aligned} $$

Hiperbolik Fonksiyonlar

Hiperbolik fonksiyonlar, sinüs ve cosinüse çok benzeyen ama birim çember yerine birim hiperbol üzerinden tanımlanan fonksiyonlardır. Bunlar Hiperbolik Sinüs (sinh), Hiperbolik Cosinüs (cosh) ve Hiperbolik Tanjant (tanh) olarak geçer. Bu fonksiyonlar aslında aşağıdaki üstel fonksiyonların kombinasyonlarıdır.

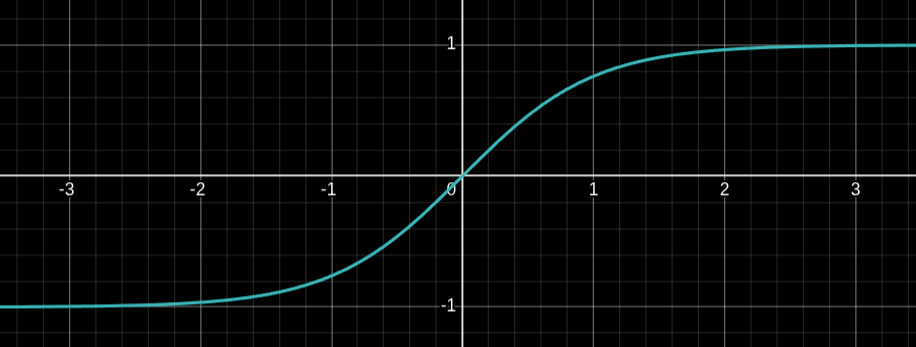
$$ \begin{aligned} & \cosh(x) = \frac{e^x + e^{-x}}{2} \\ \\ & \sinh(x) = \frac{e^x - e^{-x}}{2} \\ \\ & \tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}} \end{aligned} $$

Hiperbolik Tanjant (tanh), derin öğrenmede en yaygın kullanılan aktivasyon fonksiyonlarından biridir. Girdi değerlerini (-1, 1) aralığına sıkıştırır (squashing). Sıfır merkezli olması (yani ortalamasının sıfır olması), sinir ağlarının eğitim sürecinde gradyanların daha verimli yayılmasına yardımcı olur. Bu yüzden, Sigmoid fonksiyonuna göre genellikle daha iyi performans gösterir.

$$ \begin{aligned} \\ & y = tanh(x) \\ \end{aligned} $$

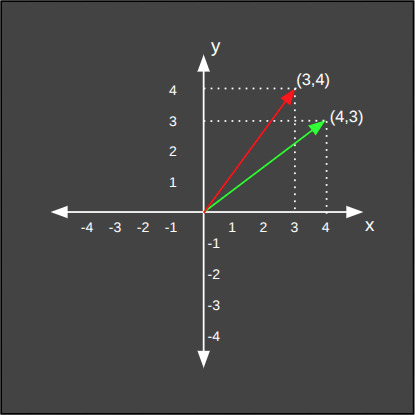
Vektörel Benzerlik ve Trigonometri

Cosinüs benzerliği olarak da anılan yöntem, özellikle doğal dil işlemede (NLP) sıkça kullanılan bir araçtır. Bu yönteme göre araba ve otomobil gibi iki kelimenin temsil edildiği iki vektörün ne kadar benzer olduğunu ölçmek için kullanılır.

$$ \begin{aligned} & \cos(\theta) = \frac{\mathbf{A} \cdot \mathbf{B}}{||\mathbf{A}|| \ ||\mathbf{B}||} \\ \\ & \upsilon_1 = [4, 3] \\ & \upsilon_2 = [3, 4] \\ & \\ & \cos(\theta) = \frac{(4*3) + (3*4)}{\sqrt{4^2 + 3^2} \ * \ \sqrt{3^2 + 4^2}} = \frac{24}{5 * 5} = 0.96 \\ & \end{aligned} $$

Yapay Zeka Gözüyle Trigonometri

Trigonometrik fonksiyonlar, yapay zeka için temel bir ifade biçimidir ve veri içindeki periyodik desenleri, rotasyonları ve salınımları modellemek için evrensel bir dil sunar. Bir robot kolunun uzamsal oryantasyonunu tanımlamaktan (ters kinematik), ses sinyallerini frekanslarına ayırmaya (Fourier analizi) ve metindeki anlamsal yönü ölçmeye (Cosinüs benzerliği) kadar kritik bir kullanım alanına sahiptirler. Trigonometri, transformer gibi en modern yapay sinir ağı mimarilerinde de halen kullanılmaya devam edilmektedir. İleride bizim inşa edeceğimiz daha bilinçli sistemlerin de temel taşı olmaya devam edecektir.

Yazar: Levent KARAGÖL