
Limit, yapay zekanın "anlık değişim" (türev) ve "sonsuzdaki davranış" (asimptotlar) gibi kritik kavramları tanımlamasını sağlayan ve Kalkülüs öğrenme algoritmalarının temelini oluşturan en temel analiz aracıdır. Bu makalede, limitin sezgisel tanımını, 0/0 gibi belirsizlik durumlarını çözme yöntemlerini ve asimptot kavramlarını inceleyeceğiz.
Limit Nedir?
Yapay zeka ve makine öğrenimi, özünde tek bir şeyle ilgilenir: Değişim. Bir modelin "öğrenmesi", yaptığı hatayı (maliyet fonksiyonu) azaltmak için parametrelerini değiştirmesi demektir. Peki, bu değişimin "anlık" hızını nasıl ölçeriz? Bir eğrinin üzerindeki tek bir noktanın eğimini nasıl buluruz?
Bu sorular bizi, bir hedefe sonsuz sayıda adımda yaklaşmaya çalışan Zeno'nun paradoksuna benzer bir yere getirir. Bir şeye asla tam olarak ulaşamasak bile, ona ne kadar yaklaştığımızı bilebilir miyiz?
İşte "Limit" kavramı burada devreye girer. Limit, bir fonksiyonun belirli bir noktadaki "davranışını", tam o noktada ne olduğuyla, hatta o noktada tanımlı olup olmadığıyla ilgilenmeden, o noktanın "hemen çevresine" bakarak anlamamızı sağlayan güçlü bir araçtır.
Limiti anlamanın en kolay yolu, onu bir yolculuk gibi düşünmektir. Diyelim ki \(f(x)\) adında bir fonksiyonumuz var. \(x\) değişkeni, \(c\) adında belirli bir değere yaklaştıkça (ancak \(c\) değerine tam olarak eşit olmadan), \(f(x)\) fonksiyonunun değeri hangi \(L\) değerine yaklaşıyor?
Eğer \(f(x)\) değeri, \(x\) değeri \(c\)'ye yaklaştıkça belirli bir \(L\) değerine (istediğimiz kadar) yakınlaşıyorsa, "\(x\), \(c\)'ye giderken \(f(x)\)'in limiti \(L\)'dir" deriz ve bunu matematiksel olarak şöyle gösteririz:
Hadi bunu bir örnek üzerinde inceleyelim. Aşağıdaki fonksiyona bakalım.
Bu fonksiyona \(x=2\) değerini vermeye çalışırsak ne olur?
Bu, matematikte "belirsiz" bir ifadedir. Fonksiyon \(x=2\) noktasında tanımlı değildir.
Peki, \(x=2\)'de tanımlı değilse, \(x\) değeri 2'ye çok yaklaştığında fonksiyon nasıl davranır? Gelin, sabırla bunu deneyelim:
| \(x\) (2'ye soldan yaklaşırken) | \(f(x)\) | \(x\) (2'ye sağdan yaklaşırken) | \(f(x)\) |
|---|---|---|---|
| 1.9 | 3.9 | 2.1 | 4.1 |
| 1.99 | 3.99 | 2.01 | 4.01 |
| 1.999 | 3.999 | 2.001 | 4.001 |
| 1.9999 | 3.9999 | 2.0001 | 4.0001 |
Gördüğümüz gibi, \(x\) değeri 2'ye ne kadar yaklaşırsa (ister soldan 1.99... ile, ister sağdan 2.00... ile), \(f(x)\) değeri de o kadar 4'e yaklaşıyor. \(f(2)\)'nin tanımsız olması umurumuzda değil! Önemli olan, o noktanın çevresindeki davranıştır.
Bu yüzden şunu cesurca yazabiliriz:
Sağdan ve Soldan Yaklaşım
Yukarıdaki tabloda \(x\)'e hem 2'den küçük değerlerle ("soldan") hem de 2'den büyük değerlerle ("sağdan") yaklaştık. Bazen bir fonksiyonun bir noktaya yaklaşırken sağdan ve soldan farklı davrandığı durumlar olur.
- Soldan Limit (\(\lim_{x \to c^-}\)): \(x\)'in \(c\)'den küçük değerler alarak \(c\)'ye yaklaşmasıdır.
- Sağdan Limit (\(\lim_{x \to c^+}\)): \(x\)'in \(c\)'den büyük değerler alarak \(c\)'ye yaklaşmasıdır.
Altın Kural: Bir fonksiyonun \(c\) noktasında bir limitinin ( \(L\) ) var olabilmesi için gerekli ve yeterli koşul, o noktadaki sağdan limitin ve soldan limitin var olması ve birbirine eşit olmasıdır. Eğer sağ ve sol limitler farklıysa (örneğin biri 5'e, diğeri -2'ye yaklaşıyorsa), o noktada "limit yoktur" deriz. Bu, fonksiyonda bir "sıçrama" veya "kopma" olduğunu gösterir.
Limit Problemlerinin Çözümü
Limit problemlerinin çözümü için soldan ve sağdan yakın sayılar vererek sonuca yaklaşmaya çalışmak geçerli bir yöntem olsa da, çoğu zaman haddinden fazla zaman alır. Bunun yerine formülde sadeleştirme ve çeşitli dönüşümlerle belirsizlikten kurtulmak, sık başvurulan alternatif bir yöntemdir.
Bunu bir örnek üzerinde görelim. Aşağıdaki limit problemine bir göz atalım.
x yerine 3 koyduğumuz zaman sonuç belirsizliğe gider. Ancak rasyonel ifadenin pay kısmı aslında \(x^2 - 3^2\) ifadesine eşittir. Bu ifadeyi \((x - 3).(x + 3)\) şeklinde yeniden yazabiliriz. Bu durumda;
şeklinde bir ifade elde ederiz. Burada pay ve paydadaki \((x-3)\) birbirini sadeleştirir ve elimizde aşağıdaki gibi bir formül ortaya çıkar.
Artık ortada bir belirsizlik olmadığına göre \(x\) yerine 3 yazarak 6 değerini bulabiliriz.
Yorum: Fonksiyonun grafiği \(y=x+3\) doğrusuyla aynıdır, ancak tam \(x=3\) noktasında bir "delik" vardır. Bizim bulduğumuz 6 değeri, o deliğin \(y\) eksenindeki koordinatıdır.
Bazen limit problemleri çok daha karmaşık gözükebilir. Örneğin aşağıdaki limit problemine bakalım.
\(x\)'e 0 değerini verdiğimizde yine belirsizlik çıkıyor. Burada bir karakök var ve bundan kurtulmamız gerekli. Bu tarz problemlerin en kolay çözüm yolu, eşleniği ile çarpma yöntemidir. Burada payı ve paydayı, rasyonel ifadenin payının eşleniği ile çarparız.
Sanki daha da karıştı gibi. Ama dikkatli bakarsak, artık rasyonel ifadenin payında \((a-b)(a+b) = a^2 - b^2\) kuralı geçerli oluyor. Burada \(a\) ifadesi \(\sqrt{x + 4}\) 'e, \(b\) ifadesi de 2'ye karşılık geliyor. O halde problemi bu şekilde tekrar yazalım.
Artık \(x\) yerine 0 yazdığımız taktirde bir belirsizlik yok. Böylece limiti hesap edebiliriz
Dikey ve Yatay Asimptot
Bir fonksiyonda \(x\) ya da \(y\) değerleri sonsuza giderken, fonksiyonun grafiği belirli bir doğruya ya da eğriye yaklaşıyor ama hiçbir zaman kesmiyorsa, bu tür durumlarda, fonksiyonun grafiğinin yaklaştığı doğruya veya eğriye "asimptot" adı verilir.
Aşağıdaki fonksiyona ve analitik düzlemdeki gösterimine bir göz atalım.
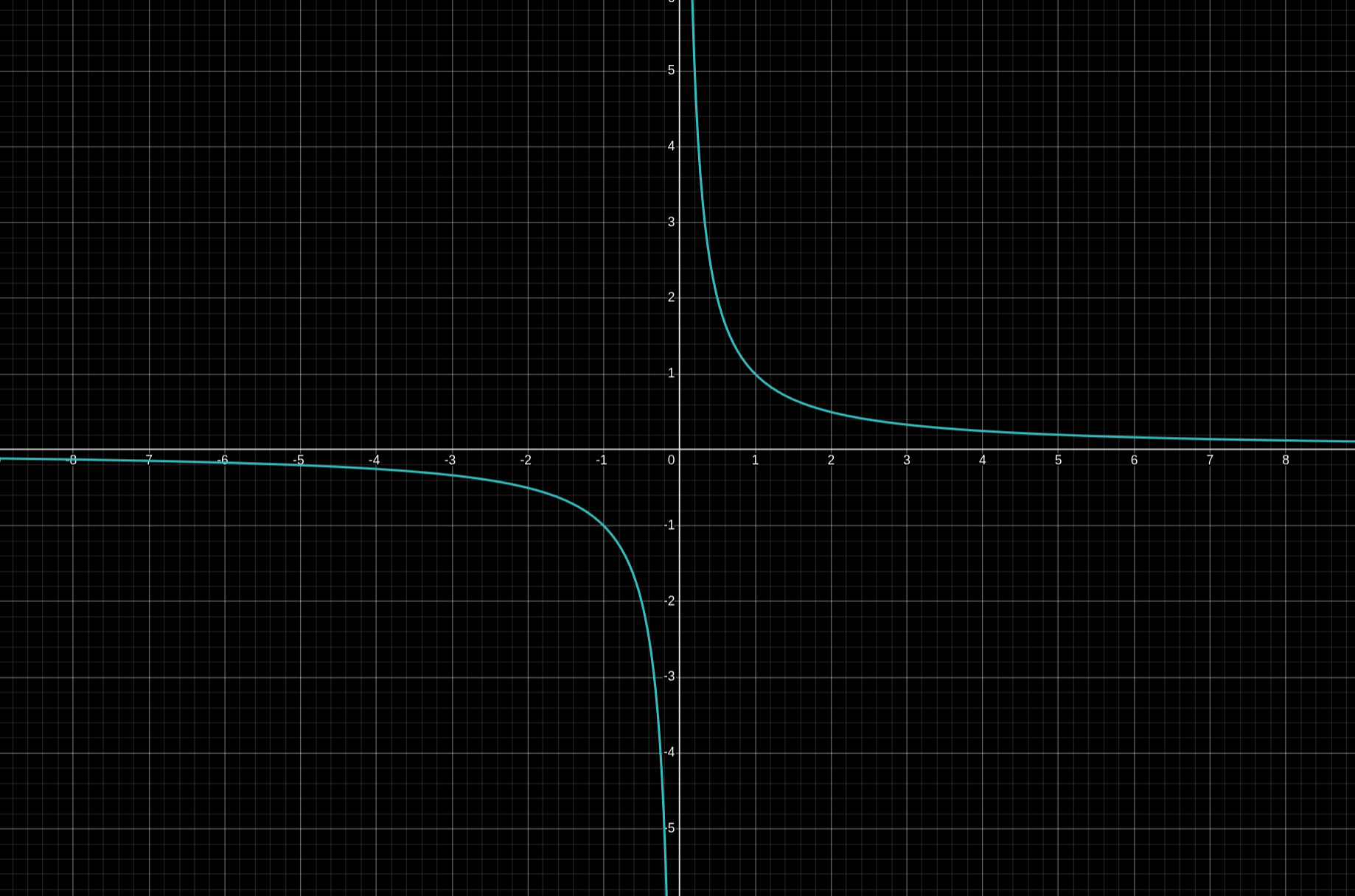
Bu fonksiyonun grafiği sonsuza dek x eksenini de, y eksenini de kesemez, sadece sonsuza dek yaklaşabilir. Bu yüzden \(x=0\) doğrusu bu fonksiyonun dikey asimptotudur. Benzer şekilde \(y=0\) doğrusu bu fonksiyonun yatay asimptotudur
Bazı fonksiyonların tek bir asimptotu vardır. Bazılarının da iki adet yatay veya dikey asimptotu vardır. Örneğin aşağıda, yapay zekada en çok kullanılan fonksiyonlardan biri olan Sigmoid fonksiyonunun grafiğini görüyoruz.
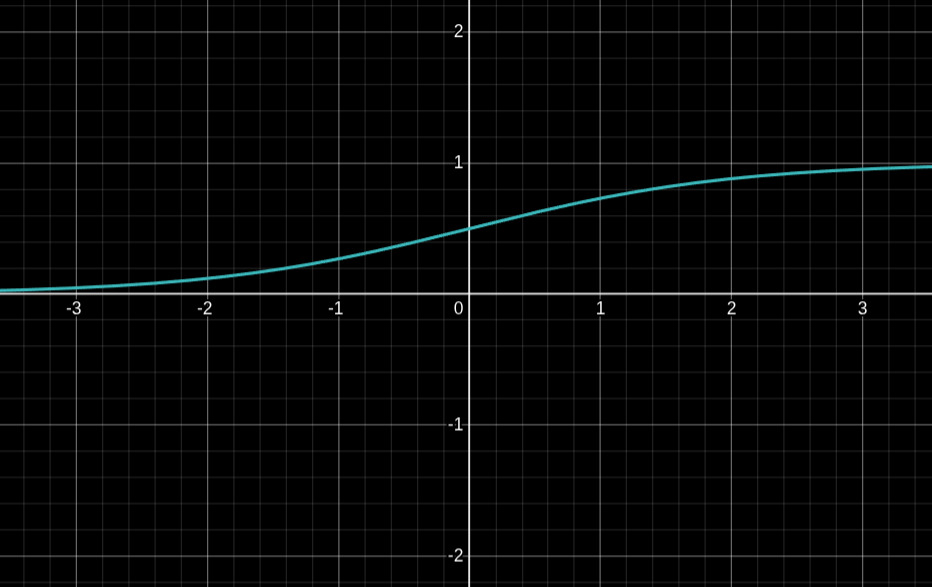
Bu fonksiyonun dikey asimptotu yoktur ancak iki adet yatay asimptotu vardır. Bunlar \(y=0\) ve \(y=1\) doğrularıdır. Çünkü fonksiyonun grafiği \(x\) sonsuza giderken \(y=1\) doğrusuna, \(x\) eksi sonsuza giderken de \(y=0\) doğrusuna yaklaşır.
Bu örnekler, asimptotları sadece bir "grafik çizim tekniği" olmaktan çıkarıp, fonksiyonların davranışsal sınırlarını tanımlayan temel bir araç haline getirir.
Yapay Zeka Gözüyle Limit
Limit kavramı, yapay zeka için tek başına bir hedef değil, "öğrenme" sürecinin matematiksel temelini oluşturan Türev'e giden yoldaki kritik ve zorunlu bir adımdır. Bir sinir ağının hatasını nasıl en aza indireceğini belirleyen Gradient Descent gibi temel optimizasyon algoritmaları, tamamen bir sonraki makalemizde inceleyeceğimiz Türev kavramına dayanır. Türev, tanımı gereği özel bir limit problemidir. Artık bu temele sahip olduğumuza göre, yapay zekanın "anlık değişimi" nasıl hesapladığını ve bu sayede nasıl "öğrendiğini" keşfetmeye, yani Türev'in dünyasına geçmeye hazırız.
Yazar: Levent KARAGÖL


