6. Polinom Fonksiyonları

16 Ekim 2025

6 dakika

118 görüntüleme

Polinom fonksiyonları, yapay zekanın doğrusal olmayan karmaşık veri desenlerini modellemesini ve bu desenlere en uygun eğrileri bularak tahminler yapmasını sağlayan esnek yapı taşlarıdır. Bu makalede, polinomların temel anatomisini, derecelerine göre sınıflandırılmasını ve bu derecenin veri modellemedeki esneklik ile aşırı öğrenme (overfitting) arasındaki hassas dengeyi nasıl kurduğunu yapay zeka perspektifiyle inceleyeceğiz.

Polinom Fonksiyonları Nedir?

Bir polinom fonksiyonu, genel olarak aşağıdaki formda ifade edilir:

$$ \begin{aligned} & P(x)=a_nx^n + a_{n−1}x^{n−1} +⋯+a_1x+a_0 \end{aligned} $$

Bu formül ilk bakışta karmaşık görünebilir, ama aslında oldukça basit parçalardan oluşur. Gelin bu parçaları birlikte inceleyelim:

Terimler (Terms): Fonksiyonu oluşturan her bir $ax^k$ parçasına terim denir. (Örn: $3x^2$)
Katsayılar (Coefficients): $ a_n, a_{n-2}, ..., a_0$ gibi değişkenlerin önündeki reel sayılardır. Modelin "öğreneceği" parametreler genellikle bu katsayılardır.
Derece (Degree): Polinomdaki en yüksek üs olan 'n' değeridir. Bu, fonksiyonun ne kadar "kıvrımlı" veya karmaşık olabileceğini belirleyen en önemli özelliktir.
Baş Katsayı (Leading Coefficient): En yüksek dereceli terimin katsayısıdır ($a_n$).
Sabit Terim (Constant Term): $x$'e bağlı olmayan, en sondaki $a_0$ terimidir. Grafiğin y-eksenini kestiği noktayı gösterir.

Polinomlar, derecelerine göre isimlendirilir ve her bir derece, kendine özgü bir grafik karakteristiği sunar.

Derece 0: Sabit Fonksiyon

Bu tür fonksiyonlarda x gibi bir değişken yoktur. Grafiği, x eksenine paralel düz bir çizgi şeklinde ilerler. Değişimi temsil etmez, bir durumun sabitliğini modeller. Aşağıda böyle bir fonksiyon görüyoruz.

$$ \begin{aligned} \\ \\ & y = 2 \end{aligned} $$

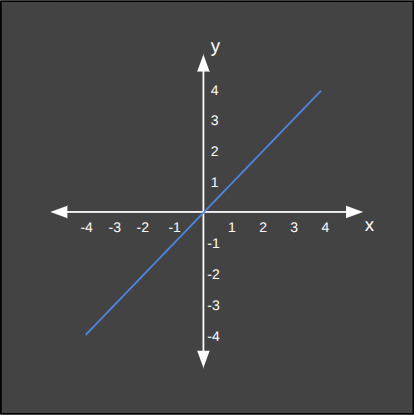
Derece 1: Lineer Fonksiyon

Yapay zekada en sık kullanılan fonksiyon türüdür. Grafiği düz bir doğrudur. Doğrusal artış veya azalışları modeller. En temel regresyon modellerinin kalbinde yer alır. $x$'in katsayısı doğrunun eğimini, sabit terim ise doğrunun y ekseni ile kesişim noktasını belirler. Aşağıda örnek iki lineer fonksiyon görüyoruz.

$$ \begin{aligned} \\ \\ & y = x \end{aligned} $$

$$ \begin{aligned} \\ \\ & y = -2x - 2 \end{aligned} $$

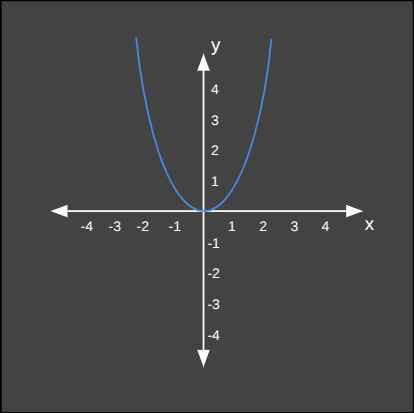
Derece 2: Parabolik Fonksiyon

Parabolik fonksiyonların adı gibi grafiği de bir paraboldür. Maliyet fonksiyonları (cost functions) gibi bir minimum veya maksimum noktası olan senaryoları modellemede kritik öneme sahiptir. Gradyan inşinin (Gradient Descent) temel mantığı, böyle bir vadinin en dibini bulma arayışıdır. Aşağıda bu fonksiyon için iki örnek görüyoruz.

$$ \begin{aligned} \\ \\ & y = x^2 \end{aligned} $$

$$ \begin{aligned} \\ \\ & y = -x^2 + 2 \end{aligned} $$

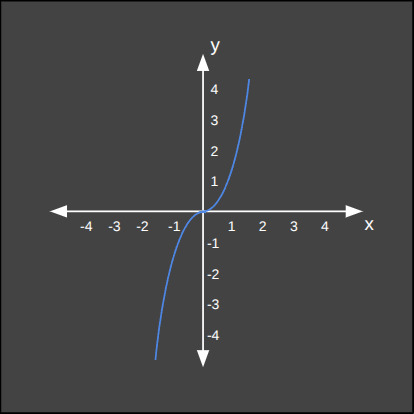
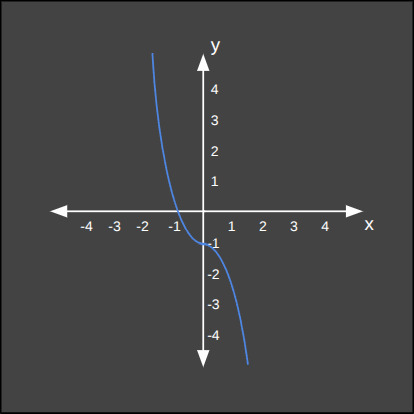
Derece 3: Kübik Fonksiyon

Üçüncü dereceden kübik fonksiyonların grafiği "S" şeklinde daha karmaşık bir eğridir. Daha fazla dönüm noktasına izin vererek daha karmaşık veri ilişkilerini modelleyebilir. Aşağıda iki kübik fonksiyon örneğini görüyoruz.

$$ \begin{aligned} \\ \\ & y = x^3 \end{aligned} $$

$$ \begin{aligned} \\ \\ & y = -x^3 - 1 \end{aligned} $$

Fonksiyon Derecesi ve Eksik/Aşırı Öğrenme

Düşük dereceli fonksiyonlar doğrusal bir hat üzerinden gittiği için veriyi eksik öğrenme (underfitting) potansiyeline sahiptir. Polinomun derecesini artırarak modelimizin esnekliğini artırabilir ve daha karmaşık veri yapılarına uyum sağlamasını sağlayabiliriz. Ancak çok yüksek bir derece, aşırı öğrenmeye (overfitting), yani modelin veriyi ezberlemesine yol açabilir. Bu, genelleme yeteneğini kaybetmesi anlamına gelir ki, bu da eğitimde yüksek skor alıp testlerde düşük skor alınmasının temel sebebidir.

Yapay sinir ağlarında kullanılan yöntem, daha düşük dereceli fonksiyonların çıkışının aktivasyon fonksiyonlarına sokularak lineer olmayan bir çıktı elde edilmesi ve bu işlemi çok sayıda ve kademeli nöronun birlikte çalışması ile birlikte daha kompleks grafiklerin modellenmesi şeklindedir.

Yapay Zeka Gözüyle Polinom Fonksiyonları

Polinom fonksiyonları yapay zeka için temel bir araç setidir ve veri içindeki doğrusal olmayan ilişkileri modellemek için yapısal bir esneklik sunar. Regresyon problemlerinde veri setlerine en uygun eğriyi tespit etmekten, özellik mühendisliğinde yeni değişkenler üretmeye kadar geniş bir kullanım alanına sahiptirler. Polinomun derecesi, modelin karmaşıklığını ayarlayan kritik bir parametre olarak işlev görür ve bu sayede makine öğrenmesindeki temel zorluklardan olan aşırı öğrenme (overfitting) ile eksik öğrenme (underfitting) arasındaki dengeyi sağlamak için bir çerçeve sunar. Zamanı geldiğinde biz de bu fonksiyonları yapay sinir ağlarımızda kullanacağız.

Yazar: Levent KARAGÖL